这次来学习一下更一般性的FFT分解

FFT的一般性分解

除了常见的 2 基底 FFT 以外，对于更一般的 $N=N_1N_2$ 问题，也有办法在理论上进行拆解，将问题化为数个 $N_1$ 与 $N_2$ 点离散傅里叶变换问题。特别的是，透过互质在数论上的特性，对于 $N_1$ 与 $N_2$ 互质的情况，可以进一步节省运算。

下面目前只讨论 $N_1N_2$ 非互质的情况。

为避免之后的符号混淆，我们先将 $N_1N_2$ 置换为 $P_1P_2$。

接着定义要拆分的问题，要拆分的问题为 $N$ 点离散傅里叶变换，将 $f\left[ n \right]$ 转换为 $F\left[ m \right]$：

$$F\left[ m \right] =\sum_{n=0}^{N-1}{f\left[ n \right] e^{-i\frac{2\pi}{N}mn}}\,\,m,n=0,1,\cdots ,N-1$$

直观地说，这个 $N$ 点离散傅里叶变换，将由 $n$ 作为参数的函数 $f\left[ n \right]$ ，转换成由 $m$ 作为参数的函数 $F\left[ m \right]$，并且 $m,n$ 都有 $N$ 个可能的数值。

待定义好要拆分的问题，便可以开始讨论如何进行拆分，基本概念是将有 $N$ 个可能的数值的 $m,n$ ，分别化为使用两个参数进行描述的函数 $m=\left[ m_1, m_2 \right], n=\left[ n_1, n_2 \right]$，并借此将原问题化为二维度离散傅里叶变换，便可使用数个较小的离散傅里叶变换问题描述整个过程。

而一种很直觉的转换方式，便是透过将 $m,n$ 分别除以 $P_2,P_1$，以商数与余数来做为参数描述 $m,n$ 的值：

$$\begin{matrix} n=n_1P_1+n_2& m=m_1+m_2P_2\\ n_1,m_1=0,1,\cdots ,P_2-1& n_2,m_2=0,1,\cdots ,P_1-1\\ \end{matrix}$$

其中 $n_1$ 作为将 $n$ 除以 $P_1$ 的商数，与作为 $m$ 除以 $P_2$ 的余数的 $m_1$ 相同，具有 $P_2$ 个可能数值，同理 $n_2$ 与 $m_2$ 有 $P_1$ 个可能数值。

将上诉的参数代换及 $N=P_1P_2$ 带入原式，可以得到：

$$F\left[ m_1+m_2P_2 \right] =\sum_{n_1=0}^{P_2-1}{\sum_{n_2=0}^{P_1-1}{f\left[ n_1P_1+n_2 \right] e^{-i\frac{2\pi}{P_1P_2}\left( m_1+m_2P_2 \right) \left( n_1P_1+n_2 \right)}}}$$

将右边的指数部分乘开并分项化简可以得到：

$$F\left[ m_1+m_2P_2 \right] =\sum_{n_1=0}^{P_2-1}{\sum_{n_2=0}^{P_1-1}{f\left[ n_1P_1+n_2 \right] e^{-i\frac{2\pi}{P_2}m_1n_1}e^{-i\frac{2\pi}{P_1}m_2n_2}e^{-i\frac{2\pi}{P_1P_2}m_1n_2}e^{-i2\pi m_2n_1}}}$$

最后透过 $e^{-i2\pi}=1$ 与 $P_1P_2=N$，可以得到：

$$F\left[ m_1+m_2P_2 \right] =\sum_{n_1=0}^{P_2-1}{\sum_{n_2=0}^{P_1-1}{f\left[ n_1P_1+n_2 \right] e^{-i\frac{2\pi}{P_2}m_1n_1}e^{-i\frac{2\pi}{P_1}m_2n_2}e^{-i\frac{2\pi}{N}m_1n_2}}}$$

观察上式，并加上括号辅助厘清运算顺序我们可以得到：

$$F\left[ m_1+m_2P_2 \right] =\sum_{n_2=0}^{P_1-1}{\left\{ \left\{ \sum_{n_1=0}^{P_2-1}{f\left[ n_1P_1+n_2 \right] e^{-i\frac{2\pi}{P_2}m_1n_1}} \right\} e^{-i\frac{2\pi}{N}m_1n_2} \right\} e^{-i\frac{2\pi}{P_1}m_2n_2}}$$

最内层的运算可以视为将双参数函数 $f[n_1,n_2]$ 中的一个参数 $n_1$，透过离散傅里叶变换取代为由 $m_1$ 描述，得到一个新函数 $G_1[m_1,n_2]$（这步因为对每个不同 $n_2$，都需要做一次将 $n_1$ 取代为 $m_1$ 的转换，共需要 $P_1$ 个 $P_2$ 点离散傅里叶变换）：

$$F\left[ m_1+m_2P_2 \right] =\sum_{n_2=0}^{P_1-1}{\left\{ G_1\left[ m_1,n_2 \right] e^{-i\frac{2\pi}{N}m_1n_2} \right\} e^{-i\frac{2\pi}{P_1}m_2n_2}}$$

下一步运算可以视为单纯的乘法，将 $G_1[m_1,n_2]$ 与 $e^{-i\frac{2\pi}{N}m_1n_2}$ 相乘，得到 $G_2[m1,n2]$（这步需要的计算量视 $\frac{m_1n_2}{N}$ 的特殊性而会有变化）：

$$F\left[ m_1+m_2P_2 \right] =\sum_{n_2=0}^{P_1-1}{G_2\left[ m_1,n_2 \right] e^{-i\frac{2\pi}{P_1}m_2n_2}}$$

最后的运算可以视为将函数 $G_2[m_1,n_2]$ 中的 $n_2$ ，透过离散傅里叶变换取代为由 $m_2$ 描述，得到一个新函数 $G_3[m_1,m_2]$（这步因为对每个不同 $m_1$，都需要做一次将 $n_2$ 取代为 $m_2$ 的转换，共需要 $P_2$ 个 $P_1$ 点离散傅里叶变换）：

$$F\left[ m\left( =m_1+m_2P_2 \right) \right] =G_3\left[ m_1,m_2 \right]$$

这样就仅使用 $P_1$ 与 $P_2$ 点离散傅里叶变换，描述了原先的 $N$ 点离散傅里叶变换。

接下来举一个实际例子帮助理解上面的流程

假设输入为

1 2 3 4 5 6 7 8

这是一个 8 点的 FFT，直接调用 scipy 库里的 fft 求得答案为：

import numpy as np
from scipy.fft import fft

np.set_printoptions(precision=2, suppress=True, linewidth=400)
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
ans = fft(x)
print("ans=", ans)

ans= [36.-0.j   -4.+9.66j -4.+4.j   -4.+1.66j -4.-0.j   -4.-1.66j -4.-4.j   -4.-9.66j]

然后用我们上面提到的一般性分解来解决这个问题，将 8 分解为 4 乘 2，也就是 $N=8,P_1=4,P_2=2$。

$$\begin{matrix} n=n_1*4+n_2& m=m_1+m_2*2\\ n_1,m_1=0,1& n_2,m_2=0,1,2,3\\ \end{matrix}$$

$$F\left[ m_1+m_2*2 \right] =\sum_{n_2=0}^3{\left\{ \left\{ \sum_{n_1=0}^1{f\left[ n_1*4+n_2 \right] e^{-i\frac{2\pi}{N_2}m_1n_1}} \right\} e^{-i\frac{2\pi}{N}m_1n_2} \right\} e^{-i\frac{2\pi}{N_1}m_2n_2}}$$

最内层是

$$G_1\left[ m_1,n_2 \right] =\sum_{n_1=0}^1{f\left[ n_1*4+n_2 \right] e^{-i\frac{2\pi}{N_2}m_1n_1}}$$

可以列出每项 $G_1$ 由哪些 $f$ 得到：

$$\begin{array}{l} G_1\left[ 0,0 \right] \Leftarrow f\left[ 0,0 \right] \&f\left[ 1,0 \right] ,G_1\left[ 1,0 \right] \Leftarrow f\left[ 0,0 \right] \&f\left[ 1,0 \right]\\ G_1\left[ 0,1 \right] \Leftarrow f\left[ 0,1 \right] \&f\left[ 1,1 \right] ,G_1\left[ 1,1 \right] \Leftarrow f\left[ 0,1 \right] \&f\left[ 1,1 \right]\\ G_1\left[ 0,2 \right] \Leftarrow f\left[ 0,2 \right] \&f\left[ 1,2 \right] ,G_1\left[ 1,2 \right] \Leftarrow f\left[ 0,2 \right] \&f\left[ 1,2 \right]\\ G_1\left[ 0,3 \right] \Leftarrow f\left[ 0,3 \right] \&f\left[ 1,3 \right] ,G_1\left[ 1,3 \right] \Leftarrow f\left[ 0,3 \right] \&f\left[ 1,3 \right]\\ \end{array}$$

然后是乘以旋转因子：

$$G_2\left[ m_1,n_2 \right] =G_1\left[ m_1,n_2 \right] e^{-i\frac{2\pi}{N}m_1n_2}$$

最后是

$$F\left[ m_1+m_2*2 \right] =G_3\left[ m_1,m_2 \right] =\sum_{n_2=0}^3{G_2\left[ m_1,n_2 \right] e^{-i\frac{2\pi}{N_1}m_2n_2}}$$

同样列出每项 $G_3$ 由哪些 $G_2$ 得到：

$$\begin{array}{l} G_3\left[ 0,0 \right] \&G_3\left[ 0,1 \right] \&G_3\left[ 0,2 \right] \&G_3\left[ 0,3 \right] \Leftarrow G_2\left[ 0,0 \right] \&G_2\left[ 0,1 \right] \&G_2\left[ 0,2 \right] \&G_2\left[ 0,3 \right]\\ G_3\left[ 1,0 \right] \&G_3\left[ 1,1 \right] \&G_3\left[ 1,2 \right] \&G_3\left[ 1,3 \right] \Leftarrow G_2\left[ 1,0 \right] \&G_2\left[ 1,1 \right] \&G_2\left[ 1,2 \right] \&G_2\left[ 1,3 \right]\\ \end{array}$$

代码如下：

import numpy as np
import cmath

np.set_printoptions(precision=2, suppress=True, linewidth=400)
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])


def DFT1(input, N, N1, N2):
    output = np.array([0 + 0j] * N)
    for n2 in range(0, N1):  # 对每个不同的n2，计算一次N2点FFT
        for m1 in range(0, N2):
            w = complex(1, 0)
            wn = cmath.exp(-1j * 2 * cmath.pi * m1 / N2)
            for n1 in range(0, N2):
                output[m1 * N1 + n2] += input[n1 * N1 + n2] * w
                w *= wn
    return output


def DFT2(input, N, N1, N2):
    output = np.array([0 + 0j] * N)
    for m1 in range(0, N2):  # 对每个不同的n1，计算一次N1点FFT
        for m2 in range(0, N1):
            w = complex(1, 0)
            wn = cmath.exp(-1j * 2 * cmath.pi * m2 / N1)
            for n2 in range(0, N1):
                output[m1 + m2 * N2] += (
                    input[m1 * N1 + n2] * w
                )  # 注意这里存储索引要写成m1+m2*N2，意为转置
                w *= wn
    return output


N = 8
N1 = 4
N2 = 2
f = x
f = DFT1(f, N, N1, N2)
print("G1=", f)
for m1 in range(0, N2):
    for n2 in range(0, N1):
        f[m1 * N1 + n2] *= cmath.exp(-1j * 2 * cmath.pi * m1 * n2 / N)
print("G2=", f)
f = DFT2(f, N, N1, N2)
print("G3=", f)

输出：

G1= [ 6.+0.j  8.+0.j 10.+0.j 12.+0.j -4.-0.j -4.-0.j -4.-0.j -4.-0.j]
G2= [ 6.  +0.j    8.  +0.j   10.  +0.j   12.  +0.j   -4.  -0.j   -2.83+2.83j -0.  +4.j    2.83+2.83j]
G3= [36.+0.j   -4.+9.66j -4.+4.j   -4.+1.66j -4.-0.j   -4.-1.66j -4.-4.j   -4.-9.66j]

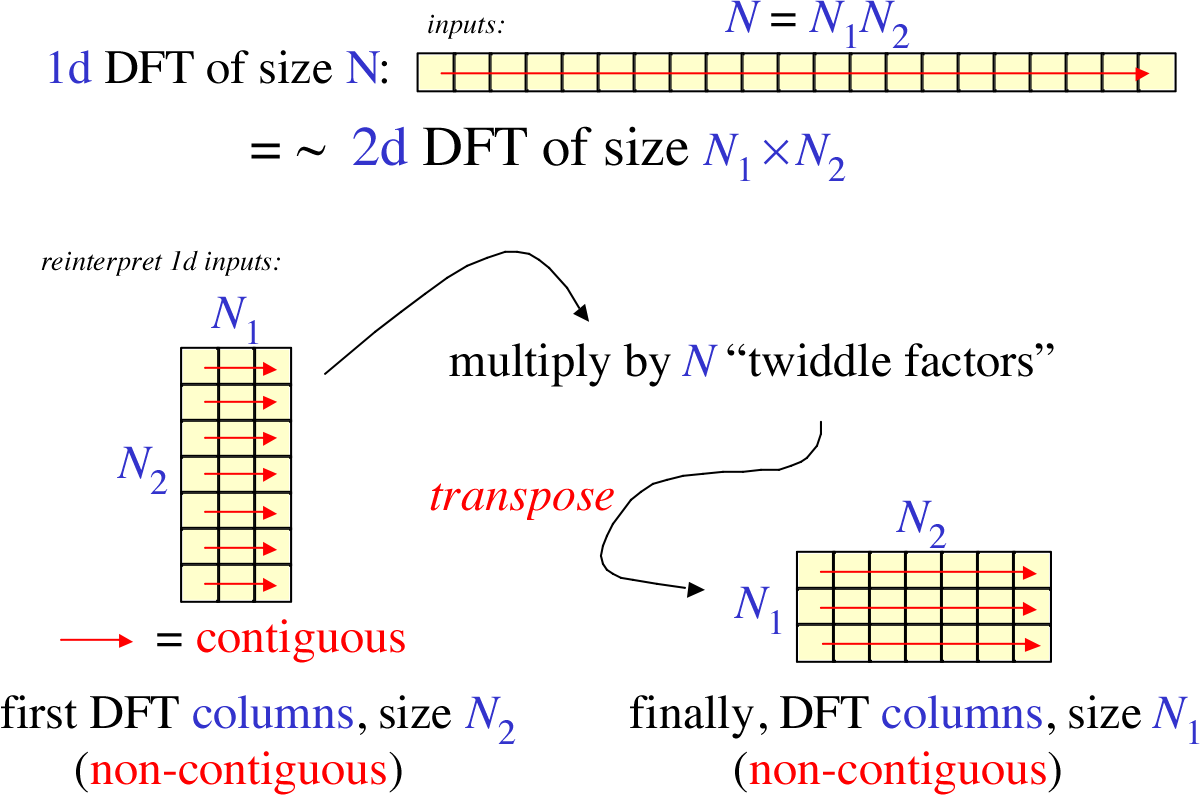
好吧，我承认光看上面的公式和代码并不能直观地理解到底做了什么，所以下面我们结合一张图来直观的展示每一步的计算

输入为：

$$f=\left[ \begin{matrix} 1& 2& 3& 4\\ 5& 6& 7& 8\\ \end{matrix} \right]$$

对输入的每一列做 DFT，也就是 4 次 2 点 DFT：

$$G_1=\left[ \begin{matrix} 6+0j& 8+0j& 10+0j& 12+0j\\ -4-0j& -4-0j& -4-0j& -4-0j\\ \end{matrix} \right]$$

对每个位置的值乘以相应的旋转因子：

$$G_2=\left[ \begin{matrix} 6+0j& 8+0j& 10+0j& 12+0j\\ -4-0j& -2.83+2.83j& 0+4j& 2.83+2.83j\\ \end{matrix} \right]$$

转置：

$$G_2=\left[ \begin{matrix} 6+0j& -4-0j\\ 8+0j& -2.83+2.83j\\ 10+0j& 0+4j\\ 12+0j& 2.83+2.83j\\ \end{matrix} \right]$$

对 $G_2$ 的每一列做 DFT，也就是 2 次 4 点 DFT ：

$$G_3=\left[ \begin{matrix} 36+0j& -4+9.66j\\ -4+4j& -4+1.66j\\ -4+0j& -4-1.66j\\ -4-4j& -4-9.66j\\ \end{matrix} \right]$$

验证代码：

import numpy as np
import cmath
from scipy.fft import fft

np.set_printoptions(precision=2, suppress=True, linewidth=400)
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
ans = fft(x)
print("ans=", ans)
res = np.array([0 + 0j] * 8)
res[::4] = fft(x[::4])
res[1::4] = fft(x[1::4])
res[2::4] = fft(x[2::4])
res[3::4] = fft(x[3::4])
print("G1=", res)
for i in range(0, 2):
    for j in range(0, 4):
        res[i * 4 + j] *= cmath.exp(-1j * 2 * cmath.pi * i * j / 8)
print("G2=", res)
res = res.reshape(2, 4).transpose().flatten()
res[::2] = fft(res[::2])
res[1::2] = fft(res[1::2])
print("G3=", res)

输出：

ans= [36.-0.j   -4.+9.66j -4.+4.j   -4.+1.66j -4.-0.j   -4.-1.66j -4.-4.j   -4.-9.66j]
G1= [ 6.-0.j  8.-0.j 10.-0.j 12.-0.j -4.-0.j -4.-0.j -4.-0.j -4.-0.j]
G2= [ 6.  +0.j    8.  +0.j   10.  +0.j   12.  +0.j   -4.  -0.j   -2.83+2.83j -0.  +4.j    2.83+2.83j]
G3= [36.+0.j   -4.+9.66j -4.+4.j   -4.+1.66j -4.+0.j   -4.-1.66j -4.-4.j   -4.-9.66j]

两份代码 $G_1,G_2,G_3$ 均相同，说明计算过程的直观体现确实如上图所示。

完整代码

import numpy as np
import cmath
from scipy.fft import fft

np.set_printoptions(precision=2, suppress=True, linewidth=400)
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
ans = fft(x)
print("ans=", ans)
res = np.array([0 + 0j] * 8)
res[::4] = fft(x[::4])
res[1::4] = fft(x[1::4])
res[2::4] = fft(x[2::4])
res[3::4] = fft(x[3::4])
print("G1=", res)
for i in range(0, 2):
    for j in range(0, 4):
        res[i * 4 + j] *= cmath.exp(-1j * 2 * cmath.pi * i * j / 8)
print("G2=", res)
res = res.reshape(2, 4).transpose().flatten()
res[::2] = fft(res[::2])
res[1::2] = fft(res[1::2])
print("G3=", res)


def DFT1(input, N, N1, N2):
    output = np.array([0 + 0j] * N)
    for n2 in range(0, N1):  # 对每个不同的n2，计算一次N2点FFT
        for m1 in range(0, N2):
            w = complex(1, 0)
            wn = cmath.exp(-1j * 2 * cmath.pi * m1 / N2)
            for n1 in range(0, N2):
                output[m1 * N1 + n2] += input[n1 * N1 + n2] * w
                w *= wn
    return output


def DFT2(input, N, N1, N2):
    output = np.array([0 + 0j] * N)
    for m1 in range(0, N2):  # 对每个不同的n1，计算一次N1点FFT
        for m2 in range(0, N1):
            w = complex(1, 0)
            wn = cmath.exp(-1j * 2 * cmath.pi * m2 / N1)
            for n2 in range(0, N1):
                output[m1 + m2 * N2] += (
                    input[m1 * N1 + n2] * w
                )  # 注意这里存储索引要写成m1+m2*N2，意为转置
                w *= wn
    return output


N = 8
N1 = 4
N2 = 2
f = x
f = DFT1(f, N, N1, N2)
print("G1=", f)
for m1 in range(0, N2):
    for n2 in range(0, N1):
        f[m1 * N1 + n2] *= cmath.exp(-1j * 2 * cmath.pi * m1 * n2 / N)
print("G2=", f)
f = DFT2(f, N, N1, N2)
print("G3=", f)

参考资料

1. 库利－图基快速傅里叶变换算法 - 维基百科，自由的百科全书
2. Cooley–Tukey FFT algorithm - Wikipedia